摘要:雙螺桿擠出機(jī)機(jī)筒內(nèi)部的流體流動(dòng)區(qū)域截面是隨時(shí)間變化的復(fù)雜三連通區(qū)域�,采取共形映射方法將這樣的三連通區(qū)域映射成不隨時(shí)間變化的圓界區(qū)域,進(jìn)一步將流動(dòng)區(qū)域變成一個(gè)不隨時(shí)間變化的柱形區(qū)域�,可大幅簡(jiǎn)化雙螺桿擠出機(jī)流體流動(dòng)問題的計(jì)算。選擇以外邊界為圓周�、內(nèi)邊界為隨時(shí)間旋轉(zhuǎn)的兩個(gè)橢圓周的平面區(qū)域上的熱傳導(dǎo)問題為研究對(duì)象,用本文方法進(jìn)行計(jì)算并比較了精確解和數(shù)值解���,計(jì)算結(jié)果表明兩解的絕對(duì)誤差較小���。本文方法可用于雙螺桿擠出機(jī)流體流動(dòng)問題的計(jì)算,并簡(jiǎn)化了計(jì)算過程�����。
引言
雙螺桿擠出機(jī)輸送效率高而且穩(wěn)定�,對(duì)于物料的處理更均勻,是塑料等高聚物生產(chǎn)的重要設(shè)備���,因此雙螺桿擠出機(jī)內(nèi)部聚合物流體的流動(dòng)性態(tài)和數(shù)值模擬是一個(gè)熱門的研究課題��。
雙螺桿擠出機(jī)內(nèi)部的流體流動(dòng)滿足的數(shù)學(xué)模型是三維的非牛頓流體動(dòng)力學(xué)方程組�����,區(qū)域復(fù)雜且隨時(shí)間變化��,因此是求解難點(diǎn)����,通常直接采用有限元[1-3]等方法或?qū)?shù)學(xué)模型降維的方法來進(jìn)行流體流動(dòng)的數(shù)值求解,但缺點(diǎn)是難以精確有效�。在此流體區(qū)域上求解雙螺桿擠出機(jī)擠出問題的另一個(gè)重要途徑是先將求解區(qū)域規(guī)則化,并在這個(gè)規(guī)則區(qū)域上進(jìn)行流體計(jì)算���。通常來說雙螺桿擠出機(jī)流體流動(dòng)區(qū)域的截面是一個(gè)三連通區(qū)域�,有3個(gè)邊界:外邊界是一個(gè)類似于8字形的外邊界�,2個(gè)內(nèi)邊界是兩根螺桿的截面邊界。因此用合適的區(qū)域變換方法將螺槽區(qū)域變成規(guī)則化的區(qū)域�����,將大大簡(jiǎn)化對(duì)雙螺桿擠出機(jī)流體的計(jì)算�。
將一個(gè)截面在一個(gè)轉(zhuǎn)動(dòng)周期中不同時(shí)刻的區(qū)域形狀經(jīng)過規(guī)則化變換變?yōu)橄嗤膱A界區(qū)域,再將雙螺桿擠出機(jī)流體流動(dòng)區(qū)域的截面轉(zhuǎn)化成圓界區(qū)域后����,求解區(qū)域非但不受時(shí)間影響,還變成了規(guī)則的����、截面為三連通圓界(形狀)區(qū)域的柱體,從而克服了求解雙螺桿擠出機(jī)流體流動(dòng)問題的主要困難���。文獻(xiàn)[4-6]研究了用區(qū)域變換方法求解單螺桿擠出機(jī)的流體流動(dòng)問題�,但其采用的方法只適用于雙連通區(qū)域同心的情況����,因此需要尋找更合適的共形映射方法來解決三連通區(qū)域的變換問題。
多連通區(qū)域的共形映射的計(jì)算方法有多種[7-9]��,通常是將區(qū)域映射到圓縫[7-8]��。本文采用文獻(xiàn)[9]的方法將三連通區(qū)域映射到圓界區(qū)域��,同時(shí)對(duì)其算法的約束條件進(jìn)行修改�����,以保證同一桿長(zhǎng)位置不同轉(zhuǎn)角的截面均映射到同樣的圓界區(qū)域�����,并更正了其中共軛調(diào)和函數(shù)求解方程式的錯(cuò)誤���。為了驗(yàn)證共形映射算法的可行性�,本文以內(nèi)部邊界曲線是兩個(gè)橢圓的雙螺桿擠出機(jī)流體流動(dòng)區(qū)域?yàn)槔蠼庠摃r(shí)變區(qū)域上的熱傳導(dǎo)方程的定解,并將數(shù)值解與精確解進(jìn)行比較�。計(jì)算結(jié)果表明,兩解的絕對(duì)誤差較小���,可以用于求解雙螺桿擠出機(jī)內(nèi)部流體流動(dòng)問題��。
1共形映射的計(jì)算
1.1 共形映射方法的理論公式
本文使用并改進(jìn)文獻(xiàn)[9]的方法�����。首先考慮一個(gè)多邊相連的有界平面區(qū)域Ωa���,其邊界分量是光滑的曲線。Ωa共形等價(jià)于圓界區(qū)域Ωc���。設(shè)f:Ωa→Ωc為共形映射���,同時(shí)令函數(shù)u=ln|f'(z)|,則u是Ωa上的調(diào)和函數(shù)��,并且滿足邊界條件(1)
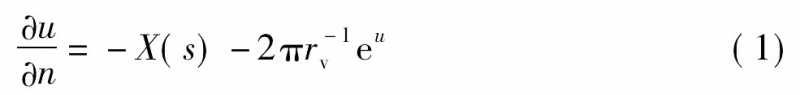
式中��,n是邊界分量,rv是對(duì)應(yīng)的圓界邊界Ωc的半徑���,s是弧長(zhǎng)參數(shù)���,X(s)是Ωa的曲率���,其值取決于s位于哪個(gè)邊界上���。
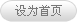
在區(qū)域邊界有尖角的情況下,將區(qū)域記為Ωp���。式(1)中X(s)在每個(gè)尖角的值是δ函數(shù)的倍數(shù)��,即X(s)=βδ(s)��,其中β是尖角的補(bǔ)角����。所以共形映射f(z)可以近似表示為
f(z)=f1((z-z0)α)
式中z0是尖角點(diǎn)的坐標(biāo)���,f1是一個(gè)單值解析函數(shù)��,α=π/(π-β)����。因此可以得到
ln|f'(z)|=(α-1)ln|z-z0|+w
式(2)中w為調(diào)和函數(shù)的光滑部分。式(2)表明調(diào)和函數(shù)u在尖角部分有對(duì)數(shù)奇點(diǎn)�����,如果減去u中所有奇異部分��,剩余部分即為在邊界上光滑的調(diào)和函數(shù)�����。利用公式(3)可以得到與尖角部分有相同奇點(diǎn)的單值函數(shù)
式(3)中�,z*是Ωp區(qū)域外部線段z0z*上除z0外的一點(diǎn),從調(diào)和函數(shù)u中去除所有奇點(diǎn){zi}后得到一個(gè)剩余的函數(shù)w即為Ωp上的調(diào)和函數(shù)���,并且w在邊界上光滑��,從而得到式(4)
u = g( z) + w
式(4)中
且w滿足邊界條件
求解如式(5)的泛函φ(w)的最小值可以得到調(diào)和函數(shù)w���。
式中,Cv表示Ωa的內(nèi)部邊界,且
得到調(diào)和函數(shù)w后�����,求解Cauchy-Riemann方程
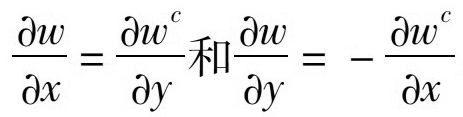
�,即可得到w的共軛調(diào)和函數(shù)wc。
注意到G(z)是解析函數(shù)����,則ln|G(z)|是從式(4)u中減去的奇異部分之和,因此f'(z)=exp(w+iwc)G(z)是解析函數(shù)�,通過對(duì)f'(z)積分可以得到共形映射f(z)�。
為了使調(diào)和函數(shù)w唯一,需要在外邊界上選取兩個(gè)點(diǎn)pi(i=1����,2(3)),從而得到限制條件式(7)
式(7)中ai為2個(gè)固定正數(shù)�,令其滿足a1+a2=2π,則式(7)可使映射f唯一�����,同時(shí)不影響目標(biāo)網(wǎng)格的形狀���,更重要的是可以使內(nèi)部邊界的形狀和大小變得相同�����。
1.2數(shù)值求解
通過有限元方法對(duì)公式(5)進(jìn)行離散來尋找函數(shù)φ(w)的最小值��。在Ωa區(qū)域打上網(wǎng)格點(diǎn)進(jìn)行三角劃分����,并在每個(gè)尖角點(diǎn)部分進(jìn)行加細(xì)處理。分別用V����、E、F來表示節(jié)點(diǎn)�����、邊和三角形的集合��,并將未知函數(shù)w離散化為τ上的分段線性函數(shù)�����。
首先�,將式(5)中的第一項(xiàng)離散為
式中H表示三角網(wǎng)格的個(gè)數(shù)�。將w的離散值排成列向量w'����,有
式中we是邊界向量,wi是內(nèi)部向量�。所以式(8)等式右邊可以寫成矩陣表達(dá)式
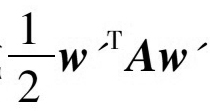
,其中系數(shù)矩陣A為對(duì)稱矩陣�����,可寫成
式中Aee�、Aii分別對(duì)應(yīng)we和wi,Aei對(duì)應(yīng)交叉部分�。
其次,將式(5)中的第二項(xiàng)離散為
式中e為三角網(wǎng)格的邊����。式(9)中g(shù)�,X(s)可以分別離散為
式(10)中,@S(e)表示在S(e)點(diǎn)的值���。值得注意的是���,
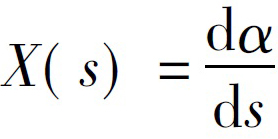
帶有方向性,因此式(9)可以寫成向量表達(dá)形式:λTwe,其中λ為系數(shù)向量�����。最后�,將式(5)中第三項(xiàng)離散為
式(11)中
式(12)中
式(13)中,l(e1)��、l(e2)分別表示p點(diǎn)兩端的邊界邊的長(zhǎng)度��。
限制條件式(7)可以離散為如下形式
式中C'i是外邊界pi與pi+1之間的節(jié)點(diǎn)集合��,且p3=p1�。
綜合公式(8)~(10)的離散過程,可得式(5)的離散形式
固定we��,則當(dāng)wi=-Aii-1Aiewe時(shí)��,φ(w')有最小值���。因此式(15)的最小值問題等價(jià)于式(16)取最小值
式中A'=Aee-AieTAii-1Aie���。
求得式(16)在約束條件式(14)下的最小值we,進(jìn)而可得到式(15)的最小值w'����。
通過求解公式(17)的最小值可以得到w的共軛調(diào)和函數(shù)
因?yàn)閒'(z)=exp(w+iwc)G(z)已知���,所以通過求解式(18)可以得到
式(18)的離散過程如下。
首先�,對(duì)于三角網(wǎng)格中頂點(diǎn)坐標(biāo)為z1,z2�,z3的三角形,令f'=(f'(z1)+f'(z2)+f'(z3))/3��,從而得到期望三角形的3個(gè)頂點(diǎn)的坐標(biāo)
將坐標(biāo)分為實(shí)部和虛部(xei�,yei)(i=1,2(3))�。
其次,該期望三角形對(duì)于式(18)離散后的實(shí)部和虛部的影響分別為
最后����,采用最小二乘法對(duì)式(20)、(21)分別求最小值��,得到最小值點(diǎn){xi}���、{yi},即得f(zk)=xk+iyk�。
因?yàn)樵谑剑?7)的計(jì)算中����,wc的值相差一個(gè)實(shí)常數(shù)�����,所以f(z)的值可以相差一個(gè)復(fù)常數(shù)�。這說明求出映射后還可以作平移和旋轉(zhuǎn)變換來保持共形性質(zhì)。圖1即為數(shù)值計(jì)算結(jié)果的圖示��,可看出對(duì)不同的轉(zhuǎn)角�����,映射后的圓界區(qū)域有較高的重合度����。
圖1流動(dòng)截面區(qū)域到圓界區(qū)域的共形映射
2實(shí)例驗(yàn)證
2.1熱傳導(dǎo)方程的變換
選擇一個(gè)熱傳導(dǎo)方程來驗(yàn)證共形映射算法的可行性。設(shè)熱傳導(dǎo)方程的求解區(qū)域是類似于圖1中的雙螺桿擠出機(jī)截面的三連通區(qū)域����,其中外邊界不隨時(shí)間變化,兩個(gè)內(nèi)邊界繞各自中心旋轉(zhuǎn)��。熱傳導(dǎo)方程如下
利用共形映射將求解區(qū)域Dt變?yōu)閳A界區(qū)域����,將自變量(x���,y)變?yōu)椋?xi;,η)�����,即得
假設(shè)此變換將Dt變?yōu)椴浑S時(shí)間變化的區(qū)域Ω�,
邊界L0、L1(t)���、L2(t)分別變?yōu)?/span>
式(24)中�,螺桿轉(zhuǎn)角θ>0,(ξ�,η)∈Ω。式(24)可以通過有限元方法計(jì)算求解�,共形映射和其逆映射的值以及相關(guān)導(dǎo)數(shù)值可以通過插值和變換之間的導(dǎo)數(shù)關(guān)系給出。
2.2數(shù)值計(jì)算結(jié)果
選取Dt的外邊界為圓心在原點(diǎn)���、半徑等于r的圓周��,其內(nèi)邊界L1(t)�、L2(t)分別是橢圓����,橢圓方程為
取r=2,a=0.6���,b=0.8����,c=0.8�,ω=1,則定解問題式(22)變?yōu)?/span>
式(25)中��,螺桿轉(zhuǎn)動(dòng)時(shí)間t>0�,(x,y)∈Dt��。
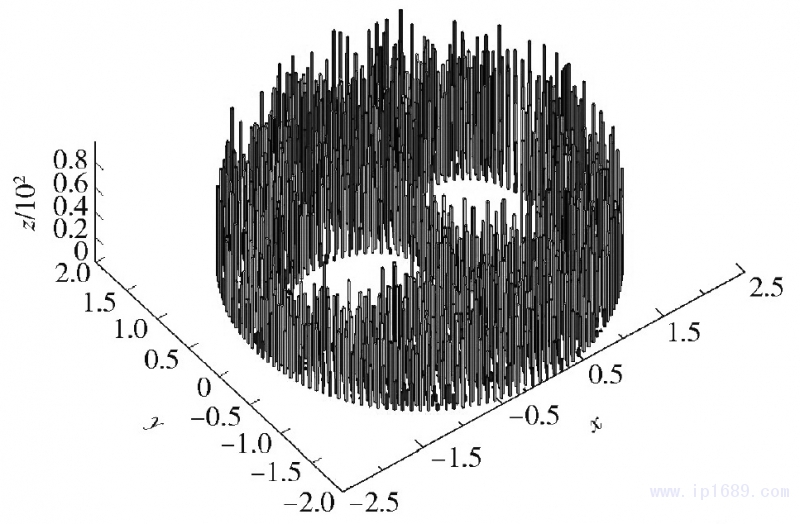
給定精確解u=e-2tsin xcos y+x2����。取邊界上初始網(wǎng)格長(zhǎng)度0.08且均勻分布的三角網(wǎng)格,區(qū)域上約有1700個(gè)網(wǎng)格點(diǎn)����,在此網(wǎng)格上計(jì)算共形映射���。數(shù)值解的求解過程為:首先對(duì)t從0~π/2進(jìn)行離散,再對(duì)每個(gè)離散的t計(jì)算共形映射�,然后利用對(duì)稱性拓展得到π/2~π對(duì)應(yīng)的離散t的共形映射,最后進(jìn)行周期延拓����,就可以得到所需的共形映射。將時(shí)間步長(zhǎng)取為π/40����,然后在映射網(wǎng)格上用有限元法求解式(25),得到t=2π時(shí)的數(shù)值解與精確解的絕對(duì)誤差如圖2所示�����。
圖2t=2π時(shí)數(shù)值解與精確解的絕對(duì)誤差
通過比較數(shù)值解和精確解可知�,其絕對(duì)誤差在0.01范圍內(nèi),表明本文算法是可行的�。
3 結(jié)論
(1)用共形映射將雙螺桿擠出機(jī)流體流動(dòng)區(qū)域的截面變?yōu)閳A界區(qū)域,可使求解區(qū)域不受轉(zhuǎn)動(dòng)的影響����,將雙螺桿擠出機(jī)流體流動(dòng)區(qū)域進(jìn)一步變換成截面為圓界區(qū)域的柱體區(qū)域,可以為雙螺桿擠出機(jī)這種復(fù)雜流體運(yùn)動(dòng)的求解提供一種精確高效的方法。
(2)利用本文方法對(duì)求解區(qū)域類似于雙螺桿擠出機(jī)截面的三連通區(qū)域的熱傳導(dǎo)問題進(jìn)行數(shù)值實(shí)驗(yàn)��,得到的數(shù)值解與精確解誤差較小���,從而證明了本文方法的可行性和有效性。














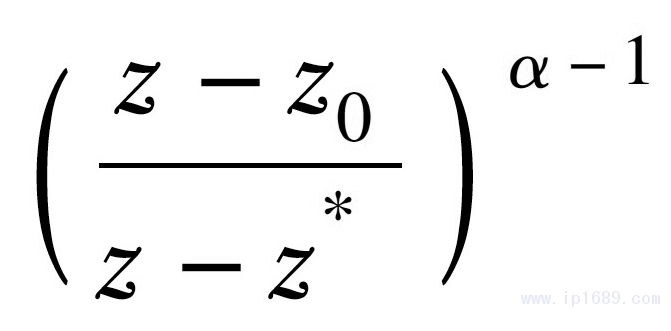
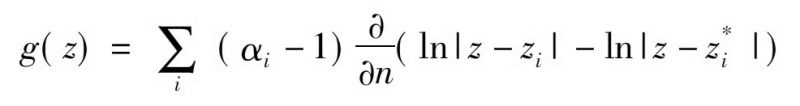
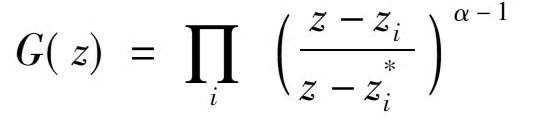
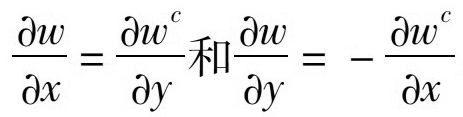
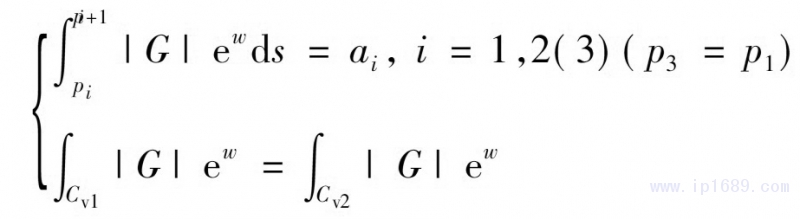
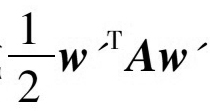
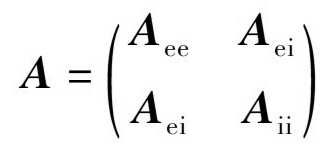
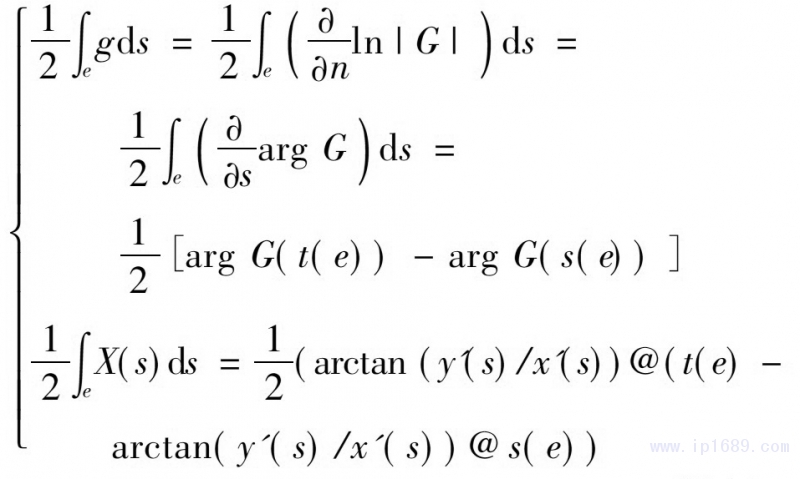
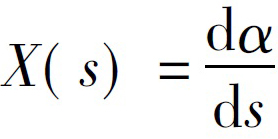
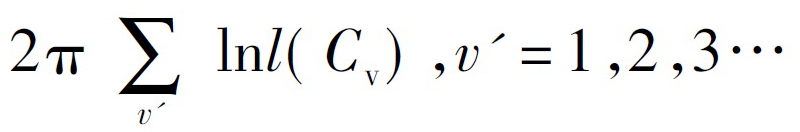
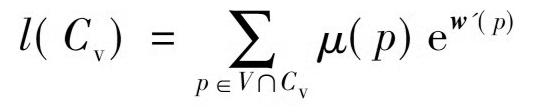
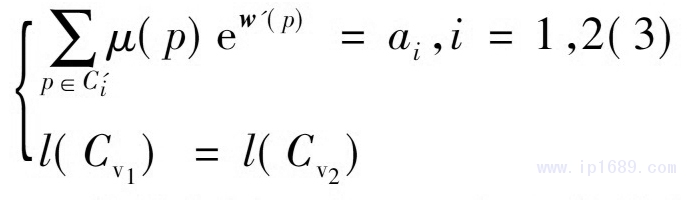
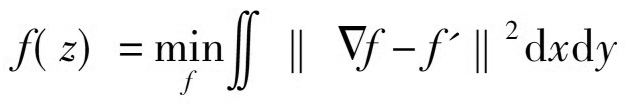
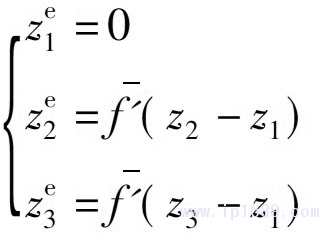
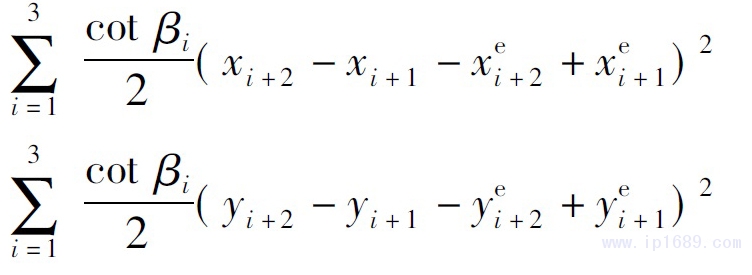

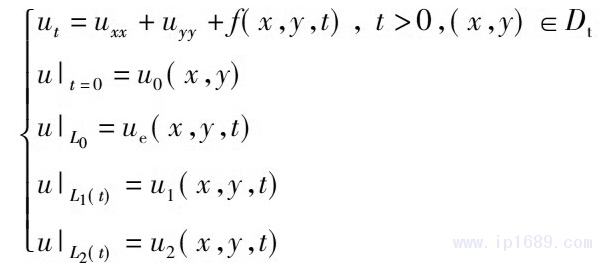
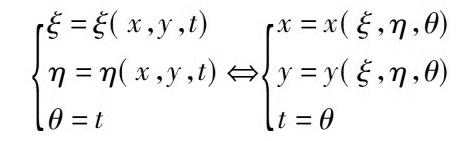
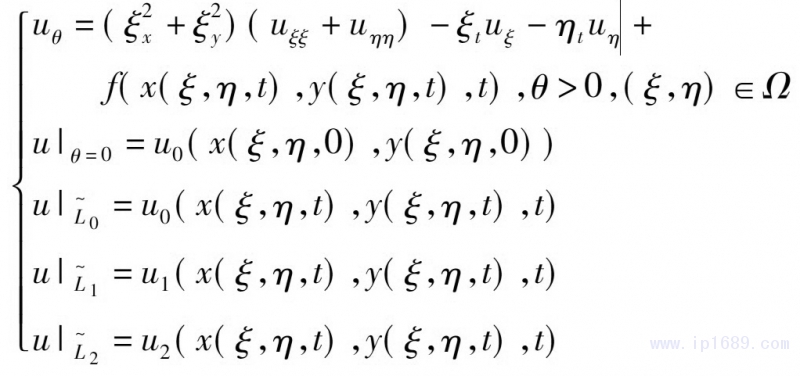
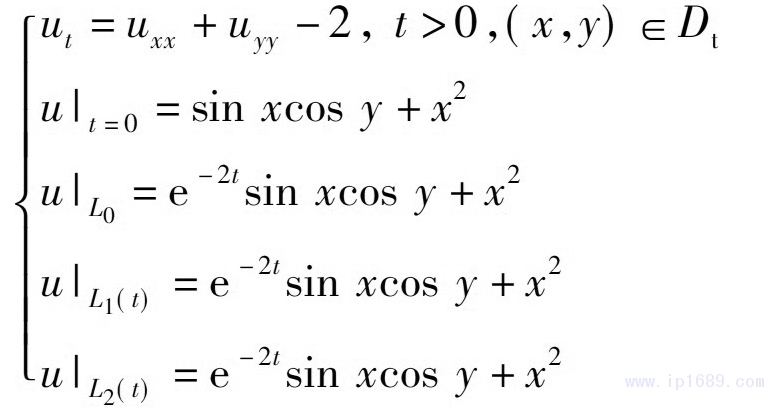

 聚砜醫(yī)療干粉吸入...
聚砜醫(yī)療干粉吸入... 塑料包裝材料的減...
塑料包裝材料的減... 汽車功能鍵觸摸蓋I...
汽車功能鍵觸摸蓋I... 高性能注塑聚丙烯...
高性能注塑聚丙烯...













